Rotation

The transformations described here are for left-handed coordinate systems, and so may be different from transformation matrices that you have seen elsewhere. For more information, see 3-D Coordinate Systems.

The following transformation rotates the point (x, y, z) around the x-axis, producing a new point (x', y', z').

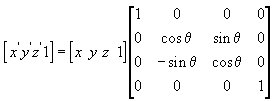
The following transformation rotates the point around the y-axis.

The following transformation rotates the point around the z-axis.

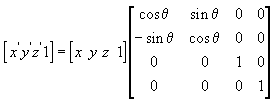
In these example matrices, the Greek letter theta (?) stands for the angle of rotation, in radians. Angles are measured clockwise when looking along the rotation axis toward the origin.

In a C++ application, use the D3DXMatrixRotationX, D3DXMatrixRotationY, and D3DXMatrixRotationZ functions supplied by the Direct3D extensions (D3DX) utility library to create rotation matrices. The following is the code for the D3DXMatrixRotationX function.

D3DXMATRIX* WINAPI D3DXMatrixRotationX
    ( D3DXMATRIX *pOut, float angle )
{
#if DBG
    if(!pOut)
        return NULL;
#endif

    float sin, cos;
    sincosf(angle, &sin, &cos);  // Determine sin and cos of angle.

    pOut->_11 = 1.0f; pOut->_12 =  0.0f;   pOut->_13 = 0.0f; pOut->_14 = 0.0f;
    pOut->_21 = 0.0f; pOut->_22 =  cos;    pOut->_23 = sin;  pOut->_24 = 0.0f;
    pOut->_31 = 0.0f; pOut->_32 = -sin;    pOut->_33 = cos;  pOut->_34 = 0.0f;
    pOut->_41 = 0.0f; pOut->_42 =  0.0f;   pOut->_43 = 0.0f; pOut->_44 = 1.0f;

    return pOut;
}