3-D Coordinate Systems

Typically 3-D graphics applications use two types of Cartesian coordinate systems: left-handed and right-handed. In both coordinate systems, the positive x-axis points to the right, and the positive y-axis points up. You can remember which direction the positive z-axis points by pointing the fingers of either your left or right hand in the positive x-direction and curling them into the positive y-direction. The direction your thumb points, either toward or away from you, is the direction that the positive z-axis points for that coordinate system. The following illustration shows these two coordinate systems.

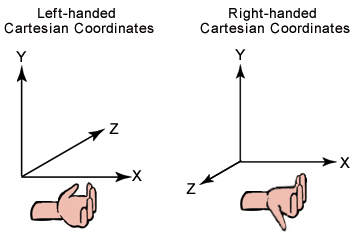
Microsoft?Direct3D?uses a left-handed coordinate system. If you are porting an application that is based on a right-handed coordinate system, you must make two changes to the data passed to Direct3D.

• Flip the order of triangle vertices so that the system traverses them clockwise from the front. In other words, if the vertices are v0, v1, v2, pass them to Direct3D as v0, v2, v1.
• Use the view matrix to scale world space by -1 in the z-direction. To do this, flip the sign of the _31, _32, _33, and _34 member of the D3DMATRIX structure that you use for your view matrix.

To obtain what amounts to a right-handed world, use the D3DXMatrixPerspectiveRH and D3DXMatrixOrthoRH functions to define the projection transform. However, be careful to use the corresponding D3DXMatrixLookAtRH function, reverse the backface-culling order, and lay out the cube maps accordingly.

Although left-handed and right-handed coordinates are the most common systems, there is a variety of other coordinate systems used in 3-D software. For example, it is not unusual for 3-D modeling applications to use a coordinate system in which the y-axis points toward or away from the viewer, and the z-axis points up. In this case, right-handedness is defined as any positive axis (x, y, or z) pointing toward the viewer. Left-handedness is defined as any positive axis (x, y, or z) pointing away from the viewer. If you are porting a left-handed modeling application where the z-axis points up, you must do a rotation on all the vertex data in addition to the previous steps.

The essential operations performed on objects defined in a 3-D coordinate system are translation, rotation, and scaling. You can combine these basic transformations to create a transform matrix. For details, see 3-D Transformations.

When you combine these operations, the results are not commutative - the order in which you multiply matrices is important.