3-D Transformations

In applications that work with 3-D graphics, you can use geometrical transformations to do the following:

• Express the location of an object relative to another object.
• Rotate and size objects.
• Change viewing positions, directions, and perspectives.

You can transform any point (x,y,z) into another point (x', y', z') using a 4 by 4 matrix.

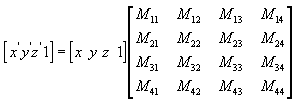
Perform the following operations on (x, y, z) and the matrix to produce the point (x', y', z').

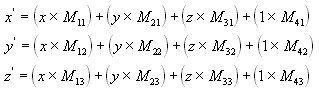
The most common transformations are translation, rotation, and scaling. You can combine the matrices that produce these effects into a single matrix to calculate several transformations at once. For example, you can build a single matrix to translate and rotate a series of points. For more information, see Matrix Concatenation.

Matrices are written in row-column order. A matrix that evenly scales vertices along each axis, known as uniform scaling, is represented by the following matrix using mathematical notation.

In C++, Microsoft?Direct3D?declares matrices as a two-dimensional array, using the D3DMATRIX structure. The following example shows how to initialize a D3DMATRIX structure to act as a uniform scaling matrix.

// In this example, s is a variable of type float.

D3DMATRIX scale = {
    s,               0.0f,            0.0f,            0.0f,
    0.0f,            s,               0.0f,            0.0f,
    0.0f,            0.0f,            s,               0.0f,
    0.0f,            0.0f,            0.0f,            1.0f
};